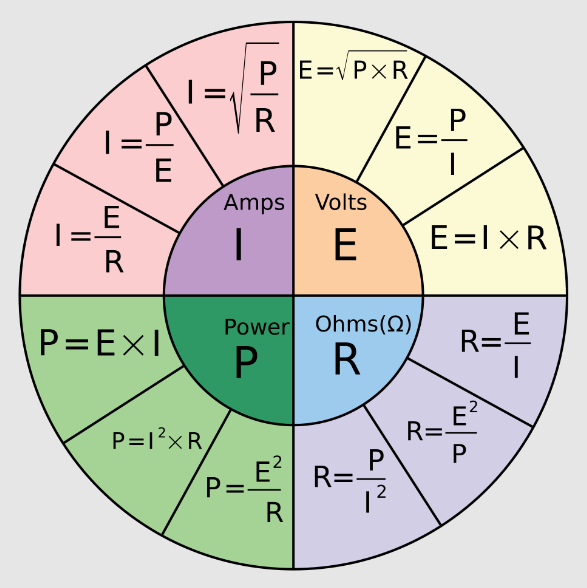
Ohms Law Calculator

Ohms Law Calculator Formula Chart , source : wikipedia.org, github.com

Introduction:

Ohm's Law, named after the German physicist Georg Simon Ohm, is a fundamental principle in electronics and electrical engineering. It describes the relationship between voltage, current, and resistance in an electrical circuit. This comprehensive guide provides a thorough understanding of Ohm's Law, including its principles, formulas, practical examples, and free software tools for analysis and calculation.

1. Principles of Ohm's Law:

Ohm's Law states that the current ( I ) flowing through a conductor between two points is directly proportional to the voltage ( V ) across the conductor and inversely proportional to the resistance ( R ) of the conductor, as expressed by the formula:

V = I  x  R 

I  = V/R

R = V/I

P = V x I or I^2*R

*see formula chart above

This relationship is fundamental to understanding how voltage, current, and resistance interact in electrical circuits.

2. Formulas of Ohm's Law:

Ohm's Law can be expressed in three different forms, each solving for one of the variables ( V ,  I , or  R ):

- Voltage (V) = Current (I) × Resistance (R)

- Current (I) = Voltage (V) ÷ Resistance (R)

- Resistance (R) = Voltage (V) ÷ Current (I)

These formulas are essential for calculating voltage, current, and resistance in electrical circuits.

3. Practical Examples of Ohm's Law:

Ohm's Law is applied in various practical scenarios to analyze and design electrical circuits. Some examples include:

- Calculating the current flowing through a resistor given its resistance and the applied voltage.

- Determining the voltage drop across a resistor in a series circuit.

- Finding the resistance of a resistor based on the voltage applied and the current flowing through it.

4. Free Software Tools for Ohm's Law Analysis:

Several free software tools are available for analyzing and calculating electrical circuits based on Ohm's Law:

- Circuit Simulator: Online circuit simulators such as Tinkercad and CircuitLab allow users to design and simulate electronic circuits, including resistors, voltage sources, and current sources, to analyze circuit behavior based on Ohm's Law.

- SPICE Software: SPICE (Simulation Program with Integrated Circuit Emphasis) software packages like LTspice and Ngspice provide powerful tools for simulating and analyzing electronic circuits, including complex circuits with multiple components and nonlinear elements.

- Calculator Apps:  Numerous smartphone apps and web-based calculators are available for performing quick calculations based on Ohm's Law, allowing users to determine voltage, current, and resistance values in real-time.

One of free web Ohms Law Calculator online from Github, written in Javascript , https://joshmatthew.github.io/ohms-law-calculator/

Conclusion:

Ohm's Law serves as a cornerstone principle in electronics and electrical engineering, providing a fundamental understanding of the relationship between voltage, current, and resistance in electrical circuits. By applying Ohm's Law and utilizing free software tools for analysis and calculation, engineers, students, and hobbyists can design, simulate, and troubleshoot electronic circuits with precision and efficiency. With its simplicity and versatility, Ohm's Law continues to be an indispensable tool in the study and practice of electrical engineering.

resistors in series and parallel

When resistors are connected in series, their equivalent resistance

${𝑅}_{\text{eq}}$ can be calculated using the formula:

${𝑅}_{\text{eq}}={𝑅}_1+{𝑅}_2+{𝑅}_3+\dots$

Where ${𝑅}_1,{𝑅}_2,{𝑅}_3,\dots$ are the resistances of individual resistors.

In series configuration, the resistors are connected end-to-end, creating a single path for the current to flow. As a result, the same current flows through each resistor, while the total voltage across the series combination is the sum of the voltages across each resistor.

In the diagram below, resistors ${𝑅}_1,{𝑅}_2,$ and ${𝑅}_3$ are connected in series:

To determine the equivalent resistance of the series combination, the resistances of all the resistors are simply added together to find ${𝑅}_{\text{eq}}$.

${𝑅}_{\text{eq}}={𝑅}_1+{𝑅}_2+{𝑅}_3$

This formula holds true for any number of resistors connected in series. When resistors are in series, the equivalent resistance is always equal to the sum of the individual resistances.

When resistors are connected in parallel, their equivalent resistance ${𝑅}_{\text{eq}}$ can be calculated using the formula:

Resistor in Paralllel for 2 Resitors 

$\frac{1}{{𝑅}_{\text{eq}}}=\frac{1}{{𝑅}_1}+\frac{1}{{𝑅}_2}+\frac{1}{{𝑅}_3}+\dots$

Where ${𝑅}_1,{𝑅}_2,{𝑅}_3,\dots$ are the resistances of individual resistors.

In parallel configuration, each resistor is connected across the same voltage source, creating multiple current paths. As a result, the total current flowing through the parallel combination is the sum of the currents flowing through each resistor. However, the voltage across each resistor remains the same.

In the diagram below, resistors ${𝑅}_1,{𝑅}_2,$ and ${𝑅}_3$ are connected in parallel:

To determine the equivalent resistance of the parallel combination, the reciprocal of each resistor's value is summed, and then the reciprocal of the total is taken to find ${𝑅}_{\text{eq}}$.

${𝑅}_{\text{eq}}=\frac{1}{\frac{1}{{𝑅}_1}+\frac{1}{{𝑅}_2}+\frac{1}{{𝑅}_3}}$

This formula is applicable to any number of resistors connected in parallel. When resistors are in parallel, the equivalent resistance is always less than the smallest resistance in the combination.