Simple RF Detector for 2 m

This simple circuit helps you sniff out RF radiation leaking from your transmitter, improper joints, a broken cable or equipment with poor RF shielding. The tester is designed for the 2-m amateur radio band (144-146 MHz in Europe).

The instrument has a 4-step LED readout and an audible alarm for high radiation voltages. The RF signal is picked up by an antenna and made to resonate by CI -LI. After rectifying by diode Dl, the signal is fed to a two-transistor highgain Darlington amplifier, T2T3. Assuming that a 10-inch telescopic antenna is used, the RF level scale set up for the LEDs is as follows:

When all LEDs light, the (optional) UM66 sound/melody generator chip (IC1) is also actuated and supplies an audible alarm. By changing the values of zener diodes D2, D4, D6 and D8, the step size

and span of the instrument may be changed as required. For operation in other ham or PMR bands, simply change the resonant network CI -LI.

As an example, a 5-watt handheld transceiver fitted with a half-wave telescopic antenna (G = 3.5 dBd), will produce an ERP (effective radiated power) of almost 10 watts and an e.m.f. of more than 8 volts close to your head.

Inductor LI consists of 2.5 turns of 20 SWG (approx. 1 mm dia) enamelled copper wire. The inside diameter is about 7 mm and no core is used. The associated trimmer capacitor CI is tuned for the highest number of LEDs to light at a relatively low fleldstrength put up by a 2-m transceiver transmitting at 145 MHz.

The tester is powered by a 9-V battery and draws about 15 mA when all LEDs are on. It should be enclosed in a metal case.

Noise Injector

This Circuit is primarily intended to be used by persons who want to experiment with audio. For example, you can determine whether your own audible threshold for noise is different with and without music, or whether a particular CD sounds better with a little bit of noise. However, since this circuit produces white noise, it can also be used for test measurements, such as comparing the sounds of different loudspeakers, measuring filter characteristics and so on. The measured characteristics, as shown in Figure 2, show a nearly flat amplitude distribution (averaged over 64 measurements). The effective value of the noise signal at the output is around 100 mV maximum (with both potentiometers set to maximum), measured over the frequency range of 22 Hz to 22 kHz.

The noise is generated by reverse-biasing the base-emitter junction of a PNP transistor (BC557B) so that it zeners. In our prototype, the voltage across Tl was approximately 10 V. PI is used to set the level of the generated noise so that it is just audible, following which the output level can be adjusted using the logarithmic potentiometer P2. For making measurements, PI can also be simply set to its maximum position. The noise is amplified by two opamp stages. Depending on the transistor manufacturer, or the type of transistor if you use a different type, the level of the generated noise can vary significantly. Using two amplification stages in series provides more options and considerably more bandwidth, and you can implement various filter characteristics around ICla and IClb according to your own taste. The gain of the two stages has been kept equal to ensure the maximum possible bandwidth. The amplified signal is then passed to a simple summing amplifier (IC2). We have used a stereo arrangement, in which both channels receive the same noise signal. If you want to expand on the design, you can provide each channel with its own noise generator. In this case, you will have to use a dual potentiometer for P2.

The well-known NE5532 is used for the amplifiers, but any other good dual opamp would also be satisfactory. The opamps are fed from a standard, symmetrical ±15-V supply. In order to suppress possible positive feedback via the power supply, and to reduce the effects of power supply noise (since the opamps are non-inverting), the supply for the noise diode circuit (Rl and Tl) is separately stabilised by IC3 (7812) and extra filtering for the ± 15-V supply is provided by C8 and C9. IC3 must be located as close as possible to Rl, Tl and IC1. The coupling capacitors CI and C2 are necessary to prevent the DC component of the noise signal from appearing at the outputs.

The table lists some measured characteristics of the circuit, for a bandwidth B of 22 Hz to 22 kHz and a reference level of 2V eff .

Low-Noise Microphone Amplifier

The signal from a microphone is two weak for a standard line input. This low-noise DC-coupled microphone amplifier pro¬ vides a solution for anyone who wants to connect a micro¬ phone to his or her hi-fi installation. As can be seen from the schematic diagram, a good circuit does not have to be com¬ plex. A differential amplifier is built around T1 (MAT-03E), which is a low-noise dual transistor. The combination of T2 and LED D1 forms a constant-current source for the input stage. A low-noise opamp (OP-270E) amplifies the difference signal that appears at the collectors of the dual transistor. The result is an analogue signal at line level. The bandwidth of the amplifier ranges from 1 Hz to 20 kHz. Within the audio range (20 Hz to 20 kHz), the distortion is less than 0.005 percent. Since only half of the OP-270E is used, the remaining opamp could be used in the output stage of a stereo version.

The amplifier can be powered from a stabilised, symmetrical supply with a voltage between ±12 V and ±15 V. Such sup¬ ply voltages are already present in many amplifiers.

Yagi Antenna Design

 

Yagi Antenna Design

Practical Antenna Handbook

 

1 Introduction to Radio Broadcasting and

Communications 1

2 Radio-wave Propagation 5

3 Transmission Lines 59

4 The Smith Chart 95

5 Fundamentals of Radio Antennas 123

6 High-Frequency Dipole and Other Doublet Antennas 141

7 Vertically Polarized HF Antennas 173

8 Multiband and Tunable-Wire Antennas 203

9 Longwire Directional Antennas 213

10 Hidden and Limited-Space Antennas 231

11 Directional Phased Vertical Antennas 245

12 Directional Beam Antennas 255

13 Antennas for Shortwave Reception 271

14 Large Wire Loop Antennas 287

15 Small Loop Receiving Antennas 299

16 Small Transmitting Loop Antennas 319

17 Antenna Modeling Software 327

18 VHF/UHF Transmitting and Receiving Antennas 339

19 Microwave Waveguides and Antennas 369

20 Antenna Noise Temperature 417

21 Antennas for Radio Astronomy 421

22 Adjusting, Installing, and Troubleshooting Antennas and

Transmission Lines 433

23 Antennas for Radio Direction Finding (RDF) 439

24 Impedence Matching in Antenna Systems 457

25 Mobile, Emergency, Portable, and Marine Antennas 479

26 Antennas for Low-Frequency Operation 501

27 Measurement and Adjustment Techniques 515

28 General Antenna Mechanical Construction Techniques 543

29 Grounding the Antenna: What Is a Good Ground? 573

Smith Chart Calculator

Smith Chart Simulation

VSWR:
Gain (dB):

Capacitor Calculator in Parallel

Capacitor Circuit Simulation

Capacitor C1: uF pF

Capacitor C2: uF pF

Capacitor C3: uF pF

Results:

Dipole Antenna Calculator

Frequency: Hz KHz MHz GHz THz

Results:

Resistor Color Code Calculator

Number of Bands: 4 Bands 5 Bands 6 Bands

Resistor Color Code Calculator

Resistor Calculator

Number of bands: 4 Bands 5 Bands 6 Bands

Band 1:

0 Black 1 Brown 2 Red 3 Orange 4 Yellow 5 Green 6 Blue 7 Violet 8 Grey 9 White

Band 2:

0 Black 1 Brown 2 Red 3 Orange 4 Yellow 5 Green 6 Blue 7 Violet 8 Grey 9 White

Band 3:

0 Black 1 Brown 2 Red 3 Orange 4 Yellow 5 Green 6 Blue 7 Violet 8 Grey 9 White

Multiplier:

Black x1Ω Brown x10Ω Red x100Ω Orange x1kΩ Yellow x10kΩ Green x100kΩ Blue x1MΩ Violet x10MΩ Grey x100MΩ White x1GΩ Gold x0.1Ω Silver x0.01Ω

Tolerance:

Brown ±1% Red ±2% Green ±0.5% Blue ±0.25% Violet ±0.1% Grey ±0.05% Gold ±5% Silver ±10%

Temperature Coefficient:

Brown 100ppm Red 50ppm Orange 15ppm Yellow 25ppm Blue 10ppm Violet 5ppm

Capacitors Calculator in Parallel

Formula

For capacitors in parallel, the total capacitance $C_{\text{total}}$ is given by: $C_{\text{total}} = C_1 + C_2 + C_3 + \ldots + C_n$

Ctotal​=C1​+C2​+C3​+…+Cn​​

Capacitors in Parallel Calculator

Enter Capacitor Values (µF):

Capacitors Calculator in Series

Capacitors in Series Formula

For capacitors in series, the total capacitance $C_{total}$ is given by: $\frac{1}{C_{total}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + \cdots + \frac{1}{C_n}$ Where $C_1, C_2, C_3, \ldots, C_n$ are the capacitances of the individual capacitors.

Capacitors in Series Calculator

Capacitor 1 (µF):

J Pole Antenna Design Calculator

J-Pole Antenna Calculator

Select Frequency: 144 MHz 220 MHz 440 MHz

<

Yagi Antenna Calculator

Design Frequency (MHz): Gain/Boom Length (dB): Boom Material: Metal Non-metal Reflector Spacing: DL6WU ARRL Director Element Spacing:

VSWR Calculator

VSWR Calculator

Reflection Coefficient (Γ, 0–1):

VSWR = ?

A dBm to watts conversion calculator is a useful tool for those working with radio frequency (RF) systems, telecommunications, and other electronic systems where power levels are often expressed in decibels relative to one milliwatt (dBm). We can create a simple yet functional calculator that performs this conversion and dynamically updates the interface with different colors based on the power level.

dBm to Watts Conversion Calculator

Enter Power in dBm:

Ohms Law Calculator

Ohms Law Calculator Formula Chart , source : wikipedia.org, github.com

Introduction:

Ohm's Law, named after the German physicist Georg Simon Ohm, is a fundamental principle in electronics and electrical engineering. It describes the relationship between voltage, current, and resistance in an electrical circuit. This comprehensive guide provides a thorough understanding of Ohm's Law, including its principles, formulas, practical examples, and free software tools for analysis and calculation.

1. Principles of Ohm's Law:

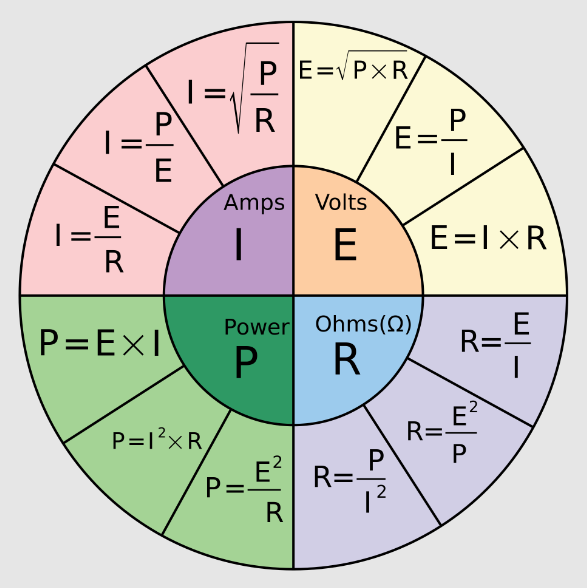
Ohm's Law states that the current ( I ) flowing through a conductor between two points is directly proportional to the voltage ( V ) across the conductor and inversely proportional to the resistance ( R ) of the conductor, as expressed by the formula:

V = I  x  R 

I  = V/R

R = V/I

P = V x I or I^2*R

*see formula chart above

This relationship is fundamental to understanding how voltage, current, and resistance interact in electrical circuits.

2. Formulas of Ohm's Law:

Ohm's Law can be expressed in three different forms, each solving for one of the variables ( V ,  I , or  R ):

- Voltage (V) = Current (I) × Resistance (R)

- Current (I) = Voltage (V) ÷ Resistance (R)

- Resistance (R) = Voltage (V) ÷ Current (I)

These formulas are essential for calculating voltage, current, and resistance in electrical circuits.

3. Practical Examples of Ohm's Law:

Ohm's Law is applied in various practical scenarios to analyze and design electrical circuits. Some examples include:

- Calculating the current flowing through a resistor given its resistance and the applied voltage.

- Determining the voltage drop across a resistor in a series circuit.

- Finding the resistance of a resistor based on the voltage applied and the current flowing through it.

4. Free Software Tools for Ohm's Law Analysis:

Several free software tools are available for analyzing and calculating electrical circuits based on Ohm's Law:

- Circuit Simulator: Online circuit simulators such as Tinkercad and CircuitLab allow users to design and simulate electronic circuits, including resistors, voltage sources, and current sources, to analyze circuit behavior based on Ohm's Law.

- SPICE Software: SPICE (Simulation Program with Integrated Circuit Emphasis) software packages like LTspice and Ngspice provide powerful tools for simulating and analyzing electronic circuits, including complex circuits with multiple components and nonlinear elements.

- Calculator Apps:  Numerous smartphone apps and web-based calculators are available for performing quick calculations based on Ohm's Law, allowing users to determine voltage, current, and resistance values in real-time.

One of free web Ohms Law Calculator online from Github, written in Javascript , https://joshmatthew.github.io/ohms-law-calculator/

Conclusion:

Ohm's Law serves as a cornerstone principle in electronics and electrical engineering, providing a fundamental understanding of the relationship between voltage, current, and resistance in electrical circuits. By applying Ohm's Law and utilizing free software tools for analysis and calculation, engineers, students, and hobbyists can design, simulate, and troubleshoot electronic circuits with precision and efficiency. With its simplicity and versatility, Ohm's Law continues to be an indispensable tool in the study and practice of electrical engineering.