With the advance of wireless communication systems and increasing importance of other wire-less applications, wide-band and low profile antennas are in great demand for both commercial and military applications. Multi-band and wideband antennas are desirable in personal communication systems,small satellite communication terminals, and other wireless applications. Wideband antennas.
Also find applications in Unmanned Aerial Vehicles (UAVs), Counter Camouflage, Concealment and Deception(CC&D), Synthetic Aperture Radar (SAR), and Ground Moving Target Indicators (GMTI).Some of these applications also require that an antenna be embedded into the air frame structure Traditionally, a wideband antenna in the low frequency wireless bands can only be achieved with heavily loaded wire antennas, which usually means different antennas are needed for different frequency bands. Recent progress in the study of fractal antennas suggests some attractive solutions for using a single small antenna operating in several frequency bands.The purpose of this article is to introduce the concept of the fractal, review the progress in fractal antenna study and implementation, com-pare different types of fractal antenna elements
and arrays and discuss the challenge and future of this new type of antenna.
Fractals
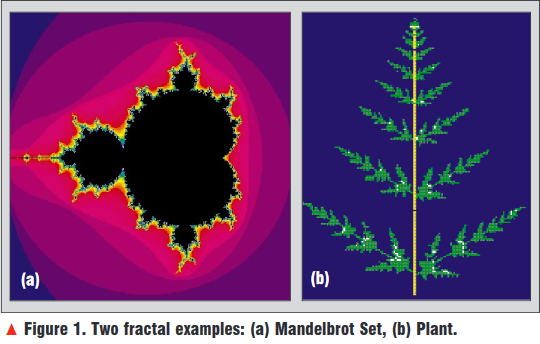
Benoit b.Mandelbrot investigated relationship between fractals and nature using the discoveries made by Gaston Julia, Pierre Fatou and Felix Hausdorff. He showed that many fractals existed in nature and that fractals could accurately model certain phenomena.He introduced new types of fractals to model more complex structures, such as trees or mountains. as shown at figure 1.
Mandelbrot defined a fractal as a rough or fragmented geometric shape that can be subdivided in parts, each of which is (at least approximately)
a reduced-size copy of the whole. (A strict mathe-matical definition is that fractal is an object whose Hausdorff-Besicovitch dimension strictly exceeds its topological dimension).Most fractal objects have self-similar shapes although there some fractal objects exist that are hardly self-sim-ilar at all. Most fractals also have infinite complexity and detail, that is, the complexity and detail of the fractals remain no matter how far you “zoom-in,” as long as you are zooming in on the right location. Also, most fractals have fractional dimensions.Fractals can model nature very well. They can be used to generate realistic landscapes or sunsets, wire-frames of mountains, rough terrain, ripples on lakes,coastline, seafloor topography, plants, and ionospheric layers. Fractals can be divided into many types. Figures1 (a, b, c) show some examples.Many theories and innovative applications for fractals are being developed. For instance, fractals have been applied in image compression, in the creation of music from pink noise, and in the analysis of high altitude lightning phenomena [2].
Fractal concepts applied to antennas
There are many ongoing efforts to develop low profileand wideband antennas such as frequency independent antennas, as reviewed in [3]. One fundamental propertyof classical frequency independent antennas is the irability to retain the same shape under certain scaling transformations, which is the self-similar property shared by many fractals. Several frequency-independent antennas can be generalized as fractal antennas [4],although they had nothing to do with fractals when first developed.
Figure 2 shows a log-periodic antenna and aspiral antenna, both of which can be categorized as fractal antennas.The general concepts of fractals can be applied to develop various antenna elements and arrays. Applying fractals to antenna elements allows for smaller, resonant antennas that are multiband/broadband and may be optimized for gain. Applying fractals to antenna arrays develops multiband/broadband arrays. The fact that most fractals have infinite complexity and detail can be used to reduce antenna size and develop low profile antennas. When antenna elements or arrays are designed with the concept of self-similarity for most fractals, they can achieve multiple frequency bands because different parts of the antenna are similar toeach other at different scales. Application of the fractional dimension of fractal structure leads to the gain optimization of wire antennas. The combination of the infinite complexity and detail and the self-similarity makes it possible to design antennas with very wideband performance. The first application of frac-tals to antenna design was thinned fractal linear and planar arrays [5]-[9], i.e., arranging the elements in a fractal pattern to reduce the number of elements in the array and obtain wideband arrays or multiband performance. An-other advantage of these fractal arrays is that the self-similarity in their geometric structure may be exploited in order to develop algorithms for rapid computation of their radiation patterns. These algorithms are based on convenient product representations for the array factors and are much quicker to calculate than the discrete Fourier transform approach.Cohen [10] was the first to develop an antenna ele-ment using the concept of fractals. He demonstrated that the concept of fractal could be used to significantly reduce the antenna size without degenerating the performance. Puente et al. [11] demonstrated the multi-band capability of fractals by studying the behavior of the Sierpinski monopole and dipole. The Sierpinski monopole displayed a similar behavior at several bands for both the input return loss and radiation pattern.Other fractals [12]-[13] have also been explored to obtain multi-band or ultra-wideband antennas.
Fractal antenna elements
The fractal concept can be used to reduce antenna size, such as the Koch dipole, Koch monopole, Koch loop,and Minkowski loop. Or, it can be used to achieve multiple bandwidth and increase bandwidth of each single band due to the self-similarity in the geometry, such as the Sierpinski dipole, Cantor slot patch, and fractal treedipole. In other designs, fractal structures are used to achieve a single very wideband response, e.g., the printed circuit fractal loop antenna. Several fractal antenna elements are presented in Figure 3.
Koch monopole and dipole— The Koch curve has been used to construct a monopole and a dipole in order to reduce antenna size.
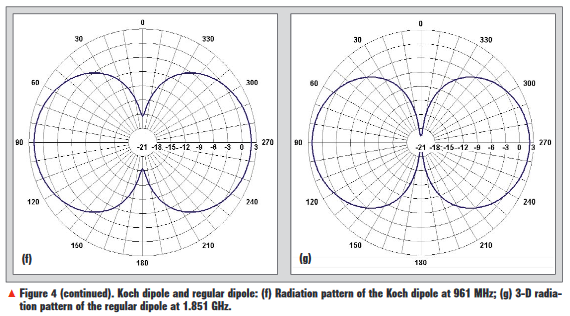
One example is shown in Figure 4. In Figure 4(a), the first resonance of a Koch dipole is at 961 MHz while that of a regular dipole with the same length is at 1851 MHz. Therefore, the length of the antenna is reduced by a fact of the 1.9. The current distribution and radiation patterns for both the Koch dipole and the regular dipole at the resonant frequencies are shown in Figure 4(b)-(f). It is worth mentioning that the radiation pattern of a Koch dipole is slightly different from that of a regular dipole because its fractal dimension is greater than 1.Koch loop and Minkowski loop— The Koch curve canalso be used to form a loop of reduced size. Another example is the Minkowski loop formed with a 90-degreebend. Both types of fractal loops can reduce the diame-ter of the loop and achieve approximately the same performance as a regular single wire loop.Sierpinski monopole and dipole— The Sierpinski gasket is a self-similar structure. In an ideal Sierpinski gasket, each of its three main parts is exactly a scaled version of the object (scaled by a factor of two). The self-similarity properties of the fractal shape are translated into its electromagnetic behavior and results in a multi-band antenna. The variation on the antenna’s flare angle shifts the operating bands, changes the impedance
level, and alters the radiation patterns.Cantor slot patch— The Cantor slot patch is another example of multiband fractal structure. This type of patch has been applied in multiband microstrip antennas and multiband frequency selective surfaces.Fractal Tree— Various fractal tree structures have been explored as antenna elements and has been found that the fractal tree usually can achieve multiple wide-band performance and reduce antenna size.Printed circuit fractal loops— The printed circuit fractal loop antenna is designed to achieve ultra wide-band or multiple wideband performance and significant-ly reduce the antenna dimensions. The antenna has a constant phase center, can be manufactured using print-ed circuit techniques, and is readily conformable to an airframe or other structure.
Fractal antenna arrays
The concept of the fractal can be applied in design and analysis of arrays by either analyzing the array using fractal theory, or placing elements in fractal arrangement, or both. Fractal arrangement of array elements can produce a thinned array and achieve multi-band performance. Examples are the Cantor linear array, Cantor ring array and Sierpinski carpet planar array, as shown in Figure 5.
Cantor linear array— Cantor linear array is based on a Cantor set with a number of design variables. When thinned, these arrays have a performance that is superior to their periodic counterparts and appear similar to or better than their random counterparts for a moderate number of elements. Figure 6 shows the calculated array factor of a five level Cantor linear array.
The largest distance as shown in Figure 6(a) is d5= 180 cm.Figure 6(b)-(g) shows the plot of array factor at different frequency bands. Itis interesting to note that there are no grating lobes at these frequencies although the distance between array elements is quite large at higher frequency bands.Cantor ring array—Similar to the Cantor linear array, Cantor ring arrays have also been explored to achieve a thinned array and achieve multiple operating frequency bands.Sierpinski carpet planar array— Sierpinski carpet planar array can be considered to be a two dimensional Cantor linear array, alsohaving multiband performance.Conclusions
The concepts of fractals can be applied to the design of antenna elements and arrays. Publications about the electromagnetic theory of fractal structures, and various fractal elements and arrays are redily available. The fact that most fractals have infinite complexity and detail makes it possible to use fractal structure to design smallsize, low profile, and low weight antennas. In addition,most fractals have self-similarity, so fractal antenna elements or arrays also can achieve multiple frequency bands due to the self-similarity between different parts of the antenna. Application of the fractional dimension of fractal structures can lead to gain optimization of wire antennas. The combination of the infinite complexity and detail and the self-similarity makes it possible to design antennas with very wideband performance.There are many interesting issues remaining to be addressed in the application of fractal structures in the design and analysis of antenna elements and arrays. For instance, when fractals are applied to image compression, adjacent parts are independent of one another.This is not the case when fractals are applied to antenna element and array design. Although they are geometrically similar, mutual coupling exists between different parts of a fractal antenna and the nature of that coupling depends on the distance and geometry of the fractal structure.
From Tehnical Feature :
X. Yang, J. Chiochetti, D. Papadopoulos and L. SusmanAPTI, Inc
No comments:
Post a Comment