Maxwell Equation's

Maxwell's Equations - The equations postulated by the Scottish physicist James Clerk Maxwell in 1864 in his article A Dynamic Theory of the Electromagnetic Field are the foundations of classical electrodynamics, classical optics and electric circuits. This set of partial differential equations describes how electric and magnetic fields are generated and altered by each other and by the influence of charges or currents. Maxwell's equations represent one of the most elegant and concise ways to state the fundamentals of electricity and magnetism. From them one can develop most of the working relationships in the field. Because of their concise statement, they embody a high level of mathematical sophistication and are therefore not generally introduced in an introductory treatment of the subject, except perhaps as summary relationships.

These basic equations of electricity and magnetism can be used as a starting point for advanced courses, but are usually first encountered as unifying equations after the study of electrical and magnetic phenomena.

where rot (or curl) is a vector operator that describes the rotation of a three- dimensional vector field,

Equation (1) is Ampere's law. It basically states that any change of the electric field over time causes a magnetic field. Equation (2) is Faraday's law of induction, which describes that any change of the magnetic field over time causes an electric field. The other two equations relate to Gauss's law. (3) states that any magnetic field is solenoid and (4) defines that the displacement current through a surface is equal to the encapsulated charge.

From Maxwell's equations and the so called material equations

it is possible to derive a second order differential equation known as the telegraph equation:

where 𝜀 is the permittivity of a dielectric medium,

          𝜎 is the electrical conductivity of a material,

          𝜇 is the permeability of a material and

        

If one assumes that the conductivity of the medium in which a wave propagates is very small (𝜎 → 0) and if one limits all signals to sinusoidal signals with an angular frequency ω, the so called wave equation can be derived:

The simplest solution to this equation is known as a plane wave propagating in loss free homogenous space. For this wave, the following condition applies:

The vectors of the electric and magnetic field strength are perpendicular to each other and mutually also to the direction of propagation , see figure below.

Consequently the electric and magnetic field strengths are connected to each other via the so called impedance of free space:

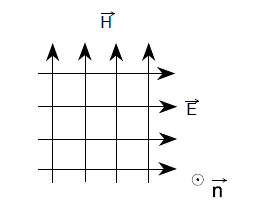Plan wave Description

Reference : Antenna Basic - Rohde & Schwarz