Feeding Phased Array Antenna

The second variation, shown in Fig. 11-2B, supposedly produces a 180° phase shift between antenna A and antenna B, when length L3 is an electrical half-wavelength. According to a much-publicized theory, the system of Fig. 11-2B

ought to produce the pattern of Fig. 11-1B—yet experience shows this claim is false. It seems that there are several problems with the system in Fig. 11-2B.

First, coax has a property called velocity factor(VF), which is the fraction of the speed of light at which signals in the cable propagate. The VF is a decimal fraction on the order of 0.66 to 0.90, depending upon the type of coax used. Unfortunately, the physical spacing between A and B is a real half-wavelength (L3 = 492/F), but the cable length is shorter by the velocity factor [L3' = (VF × 492) /F].

Consider an example. A 15-m phased vertical antenna system will have two 11-ft radiators, spaced 22 ft apart (approximately, depending upon exact frequency). If we use foam coax, with VF = 0.80, the cable length is 0.8 × 22 ft, or 17.6 ft. In other words, despite lots of publicity, the cable won’t fit between the towers! Second, the patterns shown in Fig. 11-1 are dependent upon one condition: the antenna currents are equal. If both of them are the same impedance, and are fed from the same transmitter, then it is reasonable to assume that the currents are equal—right? No, wrong! What about coax loss? Because of normal coax loss, which increases at higher frequencies, the power available to antenna Bin Fig. 11-1B is less than the power available to antenna A. Thus, the pattern will be somewhat distorted, because the current produced in Bis less than the current in A, when they should be equal.

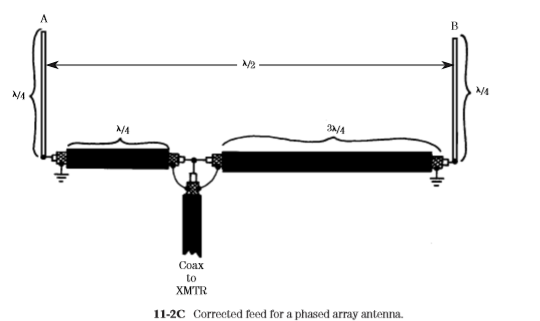
The first problem is sometimes fixed by using unequal lengths for cables L1 and L2 (Fig. 11-2A), and using it for the out-of-phase case. For example, if we make L1 one-quarter wavelength and L2 three-quarter wavelength (Fig. 11-2C), antenna A is fed with a 90° phase lag (relative to the tee connector signal), while antenna B is fed with a 270° phase shift. The result is still a 180° phase difference.

Unfortunately, we have not solved the current level problem, and may have actually made it worse by adding still more lossy cable to the system. There is still another problem that is generic to the whole class of phased verticals. Once installed, the pattern is fixed. This problem doesn’t bother most point-topoint commercial stations, or broadcasters, because they tend to transmit in only one direction. But amateurs are likely to need a rotatable pattern. Neither the antennas in Fig. 11-1A nor that in Fig. 11-1B is rotatable without a lot of effort—like changing the coax feeds, or physically digging up the verticals and repositioning them. Fortunately, there is a single solution to all three problems. Figure 11-3 shows a two-port phasing transformer made from a toroidal balun kit. Use the kind of kit that makes a 1:1 balun transformer. Although we are not making a balun, we will need enough wire to make three windings, and that is the normal case for 1:1 baluns. Amidon Associates and others make toroidal balun kits.

Wind the three coils in trifilar style, according to the kit instructions. The dots in Fig. 11-3 show the “sense” of the coils, and they are important for correct phasing; call one end the “dot end” and the other end the “plain end” to keep them separate. If the dot end of the first coil is connected to J3 (and the transmitter), then connect the dot end of the second coil to the 0° output (J1, which goes to antenna A). The third coil is connected to a DPDT RF relay or switch. In the position shown, S1 causes the antennas to be 180° out of phase. In the other position, the “sense” of the third coil is reversed, so the antennas are in phase. Another phasing method is shown in Fig. 11-4. In this scheme, two convenient, but equal, lengths of coaxial cable (L1 and L2) are used to carry RF power to the antennas. One segment (L1) is fed directly from the transmitter’s coaxial cable (L3), while the other is fed from a phasing switch. The phasing switch is used to either by

pass or insert a phase-shifting length of coaxial cable (L4). For 180° phasing use the following equation to find the length (L4):

where L is the length of L4, in feet VF is the velocity factor (a decimal fraction) FMHz is the operating frequency, in megahertz

Some people use a series of switches to select varying amounts of phasing shift from 45° to 270°. Such a switch allows them to select any number of other patterns for special situations.

Directional phased vertical antennas

THE VERTICAL ANTENNA IS A PERENNIAL FAVORITE WITH RADIO COMMUNICATIONS users. The vertical is either praised, or cursed, depending upon the luck of the owner. “DXability” is usually the criterion for judging the antenna’s quality. Some amateurs can’t get out of their backyards with a vertical, and they let everyone within earshot know that such and such a brand is no good. Yet, another person routinely works New Zealand or Australia on 15 m using exactly the same brand of vertical. The proper installation of vertical antennas is dealt with in another chapter, so, for the present, let’s look at another problem attributed to vertical antennas. That problem is that vertical antennas are omnidirectionalin the azimuth aspect; that is, they send out and receive equally well from all directions. Some people moan that this pattern dissipates their power, and gives them a weaker signal “out where it counts” (true). However, the main disadvantage of the omnidirectional pattern is noise (QRN and QRM). “QRN” is natural noise from thunderstorms and other sources. “QRM” is man-made noise, and can consist of other stations or the many assorted forms of electrical filth that pollute the airwaves. All forms of noise, however, have one thing in common: they are directional with respect to the station. In other words, if you could null signals coming from the direction of the noise source (or undesired station), you would be able to hear desired stations much better. A directional antenna performs this task, so let’s look at some vertically polarized directional antennas. Although most amateurs seem to think that the effective radiated power (ERP) increase that the directional antenna gives them is the real reason to own one, the main benefit is actually on receive. Think about it for a moment. With anywhere from 100 to 1500 W available, the increase or decrease in signal strength (due to the directivity of the antenna) results in a minimal difference on the receive end, especially during good DX conditions. If we rotate the directional pattern, to null out interference, then we usually find that the change in our signal strength perceived by the other guy is small; the S meter reading of the desired station is minimally affected; but the amplitude of the interference source is greatly attenuated! The overall effect is an apparent increase in the other guy’s signal, even though the S meter tells a slightly different story. The improvement of signal-to-noise ratio (SNR) is tremendously improved.

Directivity and phasing 

So, how does a vertical antenna owner get the benefit of directivity without the kilobuck investment that a beam or quad costs? The usual solution is to use phased verticals. AM broadcast stations, with more than one tower, are using this type of system (although for different reasons than hams). The idea is to place two or more antennas in close proximity and feed them at specific phase angles to produce a desired radiation pattern. A lot of material is available in the literature on phased vertical antenna systems, and it is far too much to be reproduced here. There are “standard patterns” dating from before World War II that are created with different spacings and different phase angles of feed current. In this chapter, we will consider only one system. Figure 11-1 shows the patterns for a pair of quarter-wavelength vertical antennas spaced a half-wavelength (180°) apart. Without getting into complex phase shifting networks, there are basically two phasings that are easily obtained: 0° (antennas in phase) and 180° (antennas out of phase with each other). When the two antennas (A and B) are fed in phase with equal currents (Fig. 111A), the radiation pattern (shown somewhat idealized here) is a bidirectional figure 8 that is directionally perpendicular to the line of centers between the two antennas; this pattern is called a broadsidepattern. A sharp null exists along the line of centers (A-B). When the antennas are fed out of phase with each other by 180° (Fig. 11-1B), the pattern rotates 90° (a quarter way around the compass) and now exhibits directivity along the line of the centers (A-B); this is the “end fire” pattern. The interference cancelling null is now perpendicular to line A-B. It should be apparent that you can select your directivity by selecting the phase angle of the feed currents in the two antennas. Figure 11-2 shows the two feeding

systems usually cited for in-phase (Fig. 11-2A) and out-of-phase (Fig. 11-2B) systems. Figure 11-2A shows the coax from the transmitter coming to a coax tee connector. From the connector to the antenna feedpoints are two lengths of coax (L1 and L2) that are equal to each other, and identical. Given the variation between coaxial cables, I suspect that it would work better if the two cables were not merely the same length (L1 = L2), but also that they came from the same roll. 

Shortened coil-loaded dipoles

The half-wavelength dipole is too long for some applications where real estate is at a premium. The solution for many operators is to use a coil-loaded shortened dipole such as shown in Fig. 6-13. A shortened dipole (i.e., one which is less than a halfwavelength) is capacitive reactance. There is no reason why the loading coil cannot be any point along the radiator, but in Figs. 6-13A and 6-13B they are placed at 0 percent and 50 percent of the element length, respectively. The reason for this procedure is that it makes the calculation of coil inductances easier, and it also represents the most common practice.

Figure 6-13C shows a table of inductive reactances as a function of the percentage of a half-wavelength, represented by the shortened radiator. It is likely that the percentage figure will be imposed on you by the situation, but the general rule is to pick the largest figure consistent with the available space. For example, suppose you have about 40 ft available for a 40-m antenna that normally needs about 65 ft for a half-wavelength. Because 39 ft is 60 percent of 65 ft, you could use this value as the design point for this antenna. Looking on the chart, a 60 percent antenna with the loading coils at the midpoint of each radiator element wants to see an inductive reactance of 700 Ω. You can rearrange the standard inductive reactance equation (XL = 6.28 FL) to the form

where LµH is the required inductance, in microhenrys F is the frequency, in hertz (Hz) XL is the inductive reactance calculated from the table in Fig. 6-13C.
Example 6-2 Calculate the inductance required for a 60 percent antenna operating on 7.25 MHz. The table requires a reactance of 700 Ωfor a loaded dipole with the coils in the center of each element (Fig. 6-15B). Solution:


The inductance calculated above is approximate, and it might have to be altered by cut-and-try methods. The loaded dipole antenna is a very sharply tuned antenna. Because of this fact, you must either confine operation to one segment of the band, or provide an antenna tuner to compensate for the sharpness of the bandwidth characteristic. However, efficiency drops, markedly, far from resonance even with a transmission line tuner. The function of the tuner is to overcome the bad effects on the transmitter, but it does not alter the basic problem. Only a variable inductor in the antenna will do that trick (at least one commercial loaded dipole once used a motor-driven inductor at the center feedpoint). Figures 6-13D and E show two methods for making a coil-loaded dipole antenna. Figure 6-13D shows a pair of commercially available loading coils especially designed for this purpose. The ones shown here are for 40 m, but other models are also available. The inductor shown in Fig. 6-13E is a section of commercial coil stock connected to a standard end or center insulator. No structural stress is assumed by the coil—all forces are applied to the insulator, which is designed to take it.

Inductance values for other length antennas can be approximated from the graph in Fig. 6-14. This graph contains three curves for coil-loaded, shortened dipoles that are 10, 50, and 90 percent of the normal half-wavelength size. Find the proposed location of the coil, as a percentage of the wire element length, along the horizontal axis. Where the vertical line from that point intersects with one of the three curves, that intersection yields the inductive reactance required (see along vertical axis). Inductances for other overall lengths can be “rough-guessed” by interpolating between the three available curves, and then validated by cut and try.

Reference : Practical Antenna Handbook  - Joseph J. Carr

Cubical quad beam antenna

The cubical quad antenna is a one-wavelength square wire loop. It was designed in the mid-1940s at radio station HCJB in Quito, Ecuador. HCJB is a Protestant missionary shortwave radio station with worldwide coverage. The location of the station is at a high altitude. This fact makes the Yagi antenna less useful than it is at lower altitudes. According to the story, HCJB originally used Yagi antennas. These antennas are fed in the center at a current loop, so the ends are high-voltage loops. In the thin air of Quito, the high voltage at the ends caused corona arcing, and that arcing periodically destroyed the tips of the Yagi elements. Station engineer Clarence Moore designed the cubical quad antenna (Fig. 12-7) to solve this problem. Because it is a full-wavelength antenna, each side being a quarter wavelength, and fed at a current loop in the center of one side, the voltage loops occur in the middle of the adjacent sides—and that reduces or eliminates the arcing. The elements can be fed in the center of a horizontal side (Figs. 12-7A and 12-8A), in the center of a vertical side (Fig. 12-8B), or at the corner (Fig. 12-8C).

The antenna shown in Fig. 12-7A is actually a quad loop rather than a cubical quad. Two or more quad loops, only one of which needs to be fed by the coax, are used to make a cubical quad antenna. If only this one element is used, then the antenna will have a figure-8 azimuthal radiation pattern (similar to a dipole). The quad loop antenna is preferred by many people over a dipole for two reasons. First, the quad loop has a smaller “footprint” because it is only a quarter-wavelength on each side (A in Fig. 12-7A). Second, the loop form makes it somewhat less susceptible to local electromagnetic interference (EMI).

The quad loop antenna (and the elements of a cubical quad beam) is mounted to spreaders connected to a square gusset plate. At one time, carpets were wrapped around bamboo stalks, and those could be used for quad antennas. Those days are gone, however, and today it is necessary to buy fiberglass quad spreaders. A number of kits are advertised in ham radio magazines.

The details for the gusset plate are shown in Fig. 12-7B. The gusset plate is made of a strong insulating material such as fiberglass or 3⁄4-in marine-grade plywood. It is mounted to a support mast using two or three large U bolts (stainless steel to prevent corrosion). The spreaders are mounted to the gusset plate using somewhat smaller U bolts (again, use stainless steel U bolts to prevent corrosion damage).

 There is a running controversy regarding how the antenna compares with other beam antennas, particularly the Yagi. Some experts claim that the cubical quad has a gain of about 1.5 to 2 dB higher than a Yagi (with a comparable boom length between the two elements). In addition, some experts claim that the quad has a lower angle of radiation. Most experts agree that the quad seems to work better at low heights above the earth’s surface, but the difference disappears at heights greater than a half-wavelength.

The quad can be used as either a single-element antenna or in the form of a beam. Figure 12-9 shows a pair of elements spaced 0.13 to 0.22 wavelengths apart. One element is the driven element, and it is connected to the coaxial-cable feedline directly. The other element is a reflector, so it is a bit longer than the driven element.

 A tuning stub is used to adjust the reflector loop to resonance.

Because the wire is arranged into a square loop, one wavelength long, the actual length varies from the naturally resonant length by about 3 percent. The driven element is about 3 percent longer than the natural resonant point. The overall lengths of the wire elements are

One method for the construction of the quad beam antenna is shown in Fig. 12-10. This particular scheme uses a 12 12-in wooden plate at the center, bamboo (or fiberglass) spreaders, and a wooden (or metal) boom. The construction must be heavy-duty in order to survive wind loads. For this reason, it is probably a better solution to buy a quad kit consisting of the spreaders and the center structural element.

More than one band can be installed on a single set of spreaders. The size of the spreaders is set by the lowest band of operation, so higher frequency bands can be accommodated with shorter loops on the same set of spreaders.

From Joseph P Carr Book " Practical Antenna HandBook"

The counterpoise longwire Antenna

The longwire antenna is an end-fed wire more than 2λ long. It provides considerable gain over a dipole, especially when a very long length can be accommodated. Although 75- to 80-m, or even 40-m longwires are a bit difficult to erect at most locations, they are well within reason at the upper end of the HF spectrum. Low-VHF band operation is also practical. Indeed, I know one fellow who lived in far southwest Virginia as a teenager, and he was able to get his family television reception for very low cost by using a TV longwire (channel 6) on top of his mountain. There are some problems with longwires that are not often mentioned.

Two problems seem to insinuate themselves into the process. First, the Zepp feed is a bit cumbersome (not everyone is enamored of parallel transmission line). Second, how do you go about actually grounding that termination resistor? If it is above ground, then the wire to ground is long, and definitely not at ground potential for RF. If you want to avoid both the straight Zepp feed system employed by most such antennas, as well as the resistor-grounding problem, then you might want to consider the counterpoise longwire antennas shown in Fig. 6-25.

A counterpoise ground is a structure that acts like a ground, but is actually electrically floating above real ground (and it is not connected to ground). A groundplane of radials is sometimes used as a counterpoise ground for vertical antennas that are mounted above actual earth ground. In fact, these antennas are often called ground plane verticals. In those antennas, the array of four (or more) radials from the shield of the coaxial cable are used as an artificial, or counterpoise, ground system. In the counterpoise longwire of Fig. 6-25A, there are two counterpoise grounds (although, for one reason or another, you might elect to use either, but not both).

One counterpoise is at the feedpoint, where it connects to the “cold” side of the transmission line. The parallel line is then routed to an antenna tuning unit (ATU), and from there to the transmitter. The other counterpoise is from the cold end of the termination resistor to the support insulator. This second counterpoise makes it possible to eliminate the earth ground connection, and all the problems that it might entail, especially in the higher end of the HF spectrum, where the wire to ground is of substantial length compared with 1λ of the operating frequency.

A slightly different scheme used to adapt the antenna to coaxial cable is shown in Fig. 6-25B. In this case, the longwire is a resonant type (nonterminated). Normally, one would expect to find this antenna fed with 450-Ω parallel transmission line. But with a λ/4 radial acting as a counterpoise, a 4:1 balun transformer can be used to effect a reasonable match to 75-Ω coaxial cable. The radial is connected to the side of the balun that is also connected to the coaxial cable shield, and the other side of the balun is connected to the radiator element.

From The Book " Practical Antenna Handbook - Joseph P. Carr"