Find the best antennas for TV, radio, and wireless. Compare top antenna deals, use free antenna calculators, follow DIY guides, and buy high-performance antennas with confidence.
Cubical quad beam antenna
The cubical quad antenna is a one-wavelength square wire loop. It was designed in the mid-1940s at radio station HCJB in Quito, Ecuador. HCJB is a Protestant missionary shortwave radio station with worldwide coverage. The location of the station is at a high altitude. This fact makes the Yagi antenna less useful than it is at lower altitudes. According to the story, HCJB originally used Yagi antennas. These antennas are fed in the center at a current loop, so the ends are high-voltage loops. In the thin air of Quito, the high voltage at the ends caused corona arcing, and that arcing periodically destroyed the tips of the Yagi elements. Station engineer Clarence Moore designed the cubical quad antenna (Fig. 12-7) to solve this problem. Because it is a full-wavelength antenna, each side being a quarter wavelength, and fed at a current loop in the center of one side, the voltage loops occur in the middle of the adjacent sides—and that reduces or eliminates the arcing. The elements can be fed in the center of a horizontal side (Figs. 12-7A and 12-8A), in the center of a vertical side (Fig. 12-8B), or at the corner (Fig. 12-8C).
The antenna shown in Fig. 12-7A is actually a quad loop rather than a cubical quad. Two or more quad loops, only one of which needs to be fed by the coax, are used to make a cubical quad antenna. If only this one element is used, then the antenna will have a figure-8 azimuthal radiation pattern (similar to a dipole). The quad loop antenna is preferred by many people over a dipole for two reasons. First, the quad loop has a smaller “footprint” because it is only a quarter-wavelength on each side (A in Fig. 12-7A). Second, the loop form makes it somewhat less susceptible to local electromagnetic interference (EMI).
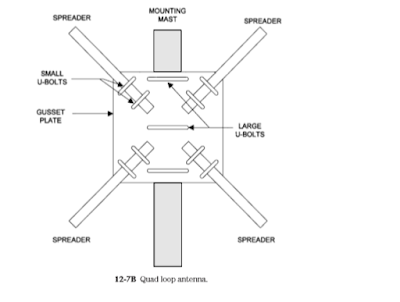
The quad loop antenna (and the elements of a cubical quad beam) is mounted to spreaders connected to a square gusset plate. At one time, carpets were wrapped around bamboo stalks, and those could be used for quad antennas. Those days are gone, however, and today it is necessary to buy fiberglass quad spreaders. A number of kits are advertised in ham radio magazines.
The details for the gusset plate are shown in Fig. 12-7B. The gusset plate is made of a strong insulating material such as fiberglass or 3⁄4-in marine-grade plywood. It is mounted to a support mast using two or three large U bolts (stainless steel to prevent corrosion). The spreaders are mounted to the gusset plate using somewhat smaller U bolts (again, use stainless steel U bolts to prevent corrosion damage).
There is a running controversy regarding how the antenna compares with other beam antennas, particularly the Yagi. Some experts claim that the cubical quad has a gain of about 1.5 to 2 dB higher than a Yagi (with a comparable boom length between the two elements). In addition, some experts claim that the quad has a lower angle of radiation. Most experts agree that the quad seems to work better at low heights above the earth’s surface, but the difference disappears at heights greater than a half-wavelength.
The quad can be used as either a single-element antenna or in the form of a beam. Figure 12-9 shows a pair of elements spaced 0.13 to 0.22 wavelengths apart. One element is the driven element, and it is connected to the coaxial-cable feedline directly. The other element is a reflector, so it is a bit longer than the driven element.
A tuning stub is used to adjust the reflector loop to resonance.
Because the wire is arranged into a square loop, one wavelength long, the actual length varies from the naturally resonant length by about 3 percent. The driven element is about 3 percent longer than the natural resonant point. The overall lengths of the wire elements are
One method for the construction of the quad beam antenna is shown in Fig. 12-10. This particular scheme uses a 12 12-in wooden plate at the center, bamboo (or fiberglass) spreaders, and a wooden (or metal) boom. The construction must be heavy-duty in order to survive wind loads. For this reason, it is probably a better solution to buy a quad kit consisting of the spreaders and the center structural element.
More than one band can be installed on a single set of spreaders. The size of the spreaders is set by the lowest band of operation, so higher frequency bands can be accommodated with shorter loops on the same set of spreaders.
From Joseph P Carr Book " Practical Antenna HandBook"
The counterpoise longwire Antenna
The longwire antenna is an end-fed wire more than 2λ long. It provides considerable gain over a dipole, especially when a very long length can be accommodated. Although 75- to 80-m, or even 40-m longwires are a bit difficult to erect at most locations, they are well within reason at the upper end of the HF spectrum. Low-VHF band operation is also practical. Indeed, I know one fellow who lived in far southwest Virginia as a teenager, and he was able to get his family television reception for very low cost by using a TV longwire (channel 6) on top of his mountain. There are some problems with longwires that are not often mentioned.
Two problems seem to insinuate themselves into the process. First, the Zepp feed is a bit cumbersome (not everyone is enamored of parallel transmission line). Second, how do you go about actually grounding that termination resistor? If it is above ground, then the wire to ground is long, and definitely not at ground potential for RF. If you want to avoid both the straight Zepp feed system employed by most such antennas, as well as the resistor-grounding problem, then you might want to consider the counterpoise longwire antennas shown in Fig. 6-25.
A counterpoise ground is a structure that acts like a ground, but is actually electrically floating above real ground (and it is not connected to ground). A groundplane of radials is sometimes used as a counterpoise ground for vertical antennas that are mounted above actual earth ground. In fact, these antennas are often called ground plane verticals. In those antennas, the array of four (or more) radials from the shield of the coaxial cable are used as an artificial, or counterpoise, ground system. In the counterpoise longwire of Fig. 6-25A, there are two counterpoise grounds (although, for one reason or another, you might elect to use either, but not both).
One counterpoise is at the feedpoint, where it connects to the “cold” side of the transmission line. The parallel line is then routed to an antenna tuning unit (ATU), and from there to the transmitter. The other counterpoise is from the cold end of the termination resistor to the support insulator. This second counterpoise makes it possible to eliminate the earth ground connection, and all the problems that it might entail, especially in the higher end of the HF spectrum, where the wire to ground is of substantial length compared with 1λ of the operating frequency.
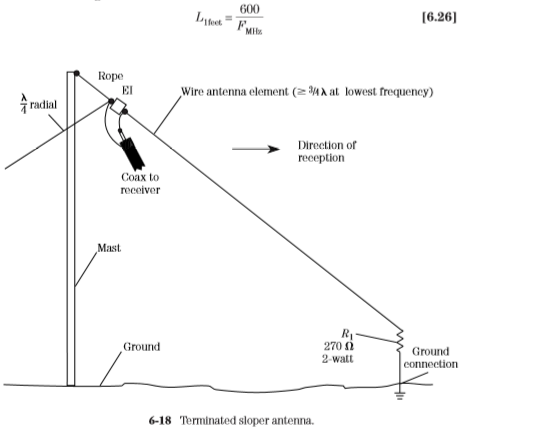
A slightly different scheme used to adapt the antenna to coaxial cable is shown in Fig. 6-25B. In this case, the longwire is a resonant type (nonterminated). Normally, one would expect to find this antenna fed with 450-Ω parallel transmission line. But with a λ/4 radial acting as a counterpoise, a 4:1 balun transformer can be used to effect a reasonable match to 75-Ω coaxial cable. The radial is connected to the side of the balun that is also connected to the coaxial cable shield, and the other side of the balun is connected to the radiator element.
From The Book " Practical Antenna Handbook - Joseph P. Carr"
Two problems seem to insinuate themselves into the process. First, the Zepp feed is a bit cumbersome (not everyone is enamored of parallel transmission line). Second, how do you go about actually grounding that termination resistor? If it is above ground, then the wire to ground is long, and definitely not at ground potential for RF. If you want to avoid both the straight Zepp feed system employed by most such antennas, as well as the resistor-grounding problem, then you might want to consider the counterpoise longwire antennas shown in Fig. 6-25.
A counterpoise ground is a structure that acts like a ground, but is actually electrically floating above real ground (and it is not connected to ground). A groundplane of radials is sometimes used as a counterpoise ground for vertical antennas that are mounted above actual earth ground. In fact, these antennas are often called ground plane verticals. In those antennas, the array of four (or more) radials from the shield of the coaxial cable are used as an artificial, or counterpoise, ground system. In the counterpoise longwire of Fig. 6-25A, there are two counterpoise grounds (although, for one reason or another, you might elect to use either, but not both).
One counterpoise is at the feedpoint, where it connects to the “cold” side of the transmission line. The parallel line is then routed to an antenna tuning unit (ATU), and from there to the transmitter. The other counterpoise is from the cold end of the termination resistor to the support insulator. This second counterpoise makes it possible to eliminate the earth ground connection, and all the problems that it might entail, especially in the higher end of the HF spectrum, where the wire to ground is of substantial length compared with 1λ of the operating frequency.
A slightly different scheme used to adapt the antenna to coaxial cable is shown in Fig. 6-25B. In this case, the longwire is a resonant type (nonterminated). Normally, one would expect to find this antenna fed with 450-Ω parallel transmission line. But with a λ/4 radial acting as a counterpoise, a 4:1 balun transformer can be used to effect a reasonable match to 75-Ω coaxial cable. The radial is connected to the side of the balun that is also connected to the coaxial cable shield, and the other side of the balun is connected to the radiator element.
From The Book " Practical Antenna Handbook - Joseph P. Carr"
Rhombic Antenna
Rhombic inverted-vee antenna
A variation on the theme is the vertically polarized rhombic of Fig. 6-23. Although sometimes called an inverted vee—not to be confused with the dipole variant of the same name—this antenna is half a rhombic, with the missing half being “mirrored” in the ground (similar to a vertical). The angle at the top of the mast (Φ) is typically ≥ 90°, and 120 to 145° is more common. Each leg (A) should be ≥λ, with the longer lengths being somewhat higher in gain, but harder to install for low frequencies. A requirement for this type of antenna is a very good ground connection. This is often accomplished by routing an underground wire between the terminating resistor ground and the feedpoint ground.
Multiband fan dipole
The basic half-wavelength dipole antenna is a very good performer, especially when cost is a factor. The dipole yields relatively good performance for practically no in
vestment. A standard half-wavelength dipole offers a bidirectional figure-8 pattern on its basic band (i.e., where the length is a half-wavelength), and a four-lobe cloverleaf pattern at frequencies for which the physical length is 3λ/2. Thus, a 40-m halfwavelength dipole produces a bidirectional pattern on 40 m, and a four-lobe cloverleaf pattern on 15 m.
The dipole is not easily multibanded without resorting to traps . One can, however, tie several dipoles to the same center insulator or balun transformer. Figure 6-24 shows three dipoles cut for different bands, operating from a common feedline and balun transformer: A1–A2, B1–B2, and C1–C2. Each of these antennas is a half-wavelength (i.e., Lfeet = 468/FMHz).
There are two points to keep in mind when building this antenna. First, try to keep the ends spread a bit apart, and second, make sure that none of the antennas is cut as a half-wavelength for a band for which another is 3λ/2. For example, if you make A1–A2 cut for 40 m, then don’t cut any of the other three for 15 m. If you do, the feedpoint impedance and the radiation pattern will be affected.
From The Book " Practical Antenna Handbook - by Joseph P. Carr"
A variation on the theme is the vertically polarized rhombic of Fig. 6-23. Although sometimes called an inverted vee—not to be confused with the dipole variant of the same name—this antenna is half a rhombic, with the missing half being “mirrored” in the ground (similar to a vertical). The angle at the top of the mast (Φ) is typically ≥ 90°, and 120 to 145° is more common. Each leg (A) should be ≥λ, with the longer lengths being somewhat higher in gain, but harder to install for low frequencies. A requirement for this type of antenna is a very good ground connection. This is often accomplished by routing an underground wire between the terminating resistor ground and the feedpoint ground.
Multiband fan dipole
The basic half-wavelength dipole antenna is a very good performer, especially when cost is a factor. The dipole yields relatively good performance for practically no in
vestment. A standard half-wavelength dipole offers a bidirectional figure-8 pattern on its basic band (i.e., where the length is a half-wavelength), and a four-lobe cloverleaf pattern at frequencies for which the physical length is 3λ/2. Thus, a 40-m halfwavelength dipole produces a bidirectional pattern on 40 m, and a four-lobe cloverleaf pattern on 15 m.
The dipole is not easily multibanded without resorting to traps . One can, however, tie several dipoles to the same center insulator or balun transformer. Figure 6-24 shows three dipoles cut for different bands, operating from a common feedline and balun transformer: A1–A2, B1–B2, and C1–C2. Each of these antennas is a half-wavelength (i.e., Lfeet = 468/FMHz).
There are two points to keep in mind when building this antenna. First, try to keep the ends spread a bit apart, and second, make sure that none of the antennas is cut as a half-wavelength for a band for which another is 3λ/2. For example, if you make A1–A2 cut for 40 m, then don’t cut any of the other three for 15 m. If you do, the feedpoint impedance and the radiation pattern will be affected.
From The Book " Practical Antenna Handbook - by Joseph P. Carr"
Vee-sloper antenna
The vee-sloper antenna is shown in Fig. 6-22. It is related to the vee beam (covered in Chap. 9), but it is built like a sloper (i.e., with the feed end of the antenna high above ground). The supporting mast height should be about half (to three-fourths) of the length of either antenna leg. The legs are sloped downward to terminating
resistors at ground level. Each wire should be longer than 1λat the lowest operating frequency. The terminating resistors should be on the order of 270 Ω(about one-half of the characteristic impedance of the antenna), with a power rating capable of dissipating one-third of the transmitter power. Like other terminating resistors, these should be noninductive (carbon composition or metal film). The advantage of this form of antenna over the vee beam is that it is vertically polarized, and the resistors are close to the earth, so they are easily grounded.
From The Book : "Practical Antenna Handbook - Joseph P. Carr"
resistors at ground level. Each wire should be longer than 1λat the lowest operating frequency. The terminating resistors should be on the order of 270 Ω(about one-half of the characteristic impedance of the antenna), with a power rating capable of dissipating one-third of the transmitter power. Like other terminating resistors, these should be noninductive (carbon composition or metal film). The advantage of this form of antenna over the vee beam is that it is vertically polarized, and the resistors are close to the earth, so they are easily grounded.
From The Book : "Practical Antenna Handbook - Joseph P. Carr"
The TCFTFD dipole
The tilted, center-fed, terminated, folded dipole(TCFTFD, also called the T2FD or TTFD) is an answer to both the noise pickup and length problems that sometimes affect other antennas. For example, a random-length wire, even with antenna tuner, will pick up considerable amounts of noise. A dipole for 40 m is 66 ft long.
This antenna was first described publicly in 1949 by Navy Captain C. L. Countryman, although the U.S. Navy tested it for a long period in California during World War II. The TCFTFD can offer claimed gains of 4 to 6 dB over a dipole, depending on the frequency and design, although 1 to 3 dB is probably closer to the mark in practice, and less than 1 dB will be obtained at some frequencies within its range (especially where the resistor has to absorb a substantial portion of the RF power). The main attraction of the TCFTFD is not its gain, but rather its broad bandedness.
In addition, the TCFTFD can also be used at higher frequencies than its design frequency. Some sources claim that the TCFTFD can be used over a 5 or 6:1 frequency range, although my own observations are that 4:1 is more likely. Nonetheless, a 40-m antenna will work over a range of 7000 to 25,000 kHz, with at least some decent performance up into the 11-m Citizen’s Band (27,000 kHz).
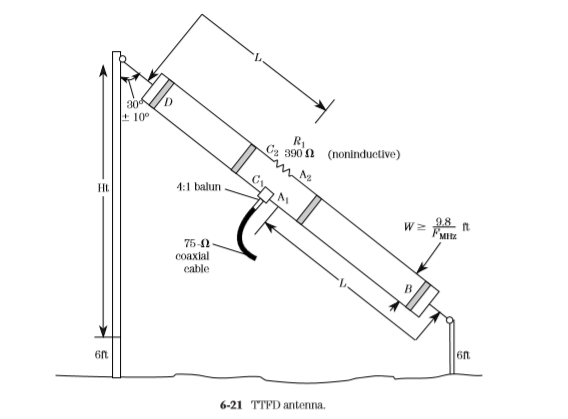
The basic TCFTFD (Fig. 6-21) resembles a folded dipole in that it has two parallel conductors of length L, spaced a distance W apart, and shorted together at the
ends. The feedpoint is the middle of one conductor, where a 4:1 balun coil and 75-Ω coaxial-cable transmission line to the transceiver are used. A noninductive, 390-Ω resistor is placed in the center of the other conductor. This resistor can be a carbon-composition (or metal-film) resistor, but it must not be a wirewound resistor or any other form that has appreciable inductance. The resistor must be able to dissipate about one-third of the applied RF power. The TCFTFD can be built from ordinary no.14 stranded antenna wire.
For a TCFTFD antenna covering 40 through 11 m, the spread between the conductors should be 191⁄2 in, while the length L is 27 ft. Note that length L includes one-half of the 19-in spread because it is measured from the center of the antenna element to the center of the end supports.
The TCFTFD is a sloping antenna, with the lower support being about 6 ft off the ground. The height of the upper support depends on the overall length of the antenna. For a 40-m design, the height is on the order of 50 ft.
The parallel wires are kept apart by spreaders. At least one commercial TCFTFD antenna uses PVC spreaders, while others use ceramic. You can use wooden dowels of between 1-in and 5⁄8-in diameter; of course, a coating of varnish (or urethane spray) is recommended for weather protection. Drill two holes, of a size sufficient to pass the wire, that are the dimension W apart (19 in for 40 m). Once the spreaders are in place, take about a foot of spare antenna wire and make jumpers to hold the dowels in place. The jumper is wrapped around the antenna wire on either side of the dowel, and then soldered.
The two end supports can be made of 1 × 2 in wood treated with varnish or urethane spray. The wire is passed through screw eyes fastened to the supports. A support rope is passed through two holes on either end of the 1 × 2 and then tied off at an end insulator.
The TCFTFD antenna is noticeably quieter than the random-length wire antenna, and somewhat quieter than the half-wavelength dipole. When the tilt angle is around 30°, the pattern is close to omnidirectional. Although a little harder to build than dipoles, it offers some advantages that ought not to be overlooked. These dimensions will suffice when the “bottom end” frequency is the 40-m band, and it will work well on higher bands.
From The Book " Practical Antenna Handbook " Joseph P. Carr
This antenna was first described publicly in 1949 by Navy Captain C. L. Countryman, although the U.S. Navy tested it for a long period in California during World War II. The TCFTFD can offer claimed gains of 4 to 6 dB over a dipole, depending on the frequency and design, although 1 to 3 dB is probably closer to the mark in practice, and less than 1 dB will be obtained at some frequencies within its range (especially where the resistor has to absorb a substantial portion of the RF power). The main attraction of the TCFTFD is not its gain, but rather its broad bandedness.
In addition, the TCFTFD can also be used at higher frequencies than its design frequency. Some sources claim that the TCFTFD can be used over a 5 or 6:1 frequency range, although my own observations are that 4:1 is more likely. Nonetheless, a 40-m antenna will work over a range of 7000 to 25,000 kHz, with at least some decent performance up into the 11-m Citizen’s Band (27,000 kHz).
The basic TCFTFD (Fig. 6-21) resembles a folded dipole in that it has two parallel conductors of length L, spaced a distance W apart, and shorted together at the
ends. The feedpoint is the middle of one conductor, where a 4:1 balun coil and 75-Ω coaxial-cable transmission line to the transceiver are used. A noninductive, 390-Ω resistor is placed in the center of the other conductor. This resistor can be a carbon-composition (or metal-film) resistor, but it must not be a wirewound resistor or any other form that has appreciable inductance. The resistor must be able to dissipate about one-third of the applied RF power. The TCFTFD can be built from ordinary no.14 stranded antenna wire.
For a TCFTFD antenna covering 40 through 11 m, the spread between the conductors should be 191⁄2 in, while the length L is 27 ft. Note that length L includes one-half of the 19-in spread because it is measured from the center of the antenna element to the center of the end supports.
The TCFTFD is a sloping antenna, with the lower support being about 6 ft off the ground. The height of the upper support depends on the overall length of the antenna. For a 40-m design, the height is on the order of 50 ft.
The parallel wires are kept apart by spreaders. At least one commercial TCFTFD antenna uses PVC spreaders, while others use ceramic. You can use wooden dowels of between 1-in and 5⁄8-in diameter; of course, a coating of varnish (or urethane spray) is recommended for weather protection. Drill two holes, of a size sufficient to pass the wire, that are the dimension W apart (19 in for 40 m). Once the spreaders are in place, take about a foot of spare antenna wire and make jumpers to hold the dowels in place. The jumper is wrapped around the antenna wire on either side of the dowel, and then soldered.
The two end supports can be made of 1 × 2 in wood treated with varnish or urethane spray. The wire is passed through screw eyes fastened to the supports. A support rope is passed through two holes on either end of the 1 × 2 and then tied off at an end insulator.
The TCFTFD antenna is noticeably quieter than the random-length wire antenna, and somewhat quieter than the half-wavelength dipole. When the tilt angle is around 30°, the pattern is close to omnidirectional. Although a little harder to build than dipoles, it offers some advantages that ought not to be overlooked. These dimensions will suffice when the “bottom end” frequency is the 40-m band, and it will work well on higher bands.
From The Book " Practical Antenna Handbook " Joseph P. Carr
Collinear “Franklin” array antenna
Perhaps the cheapest approach to very serious antenna gain is the collinear Franklin array shown in Fig. 6-20. This antenna pushes the dipole and double extended Zepp concepts even farther. It consists of a half-wavelength dipole that is center-fed with a 4:1 balun and 75-Ω coaxial cable. At each end of the dipole, there is a quarter-wavelength phase reversal stub that end-feeds another half-wavelength element. Each element is a half-wavelength (λ/2) long, and its length can be calculated from
The phase reversal stubs are a quarter-wavelength long, or one half the length calculated by Eq. 6.28.
The version of the “Collinear” shown in Fig. 6-20 has a gain of about 3 dB. There is no theoretical reason why you can’t extend the design indefinitely, but there is a practical limit set by how much wire can be held by your supports, and how much real estate you own. A 4.5-dB version can be built by adding another half-wavelength section at each end, with an intervening quarter-wavelength phase reversal stub in between each new section, and the preceding section. Once you get longer than five half-wavelengths, which provides the 4.5-dB gain, the physical size becomes a bit of a bother for most folks.
From Book Practical Antenna Handbook - Joseph P. Carr
The phase reversal stubs are a quarter-wavelength long, or one half the length calculated by Eq. 6.28.
The version of the “Collinear” shown in Fig. 6-20 has a gain of about 3 dB. There is no theoretical reason why you can’t extend the design indefinitely, but there is a practical limit set by how much wire can be held by your supports, and how much real estate you own. A 4.5-dB version can be built by adding another half-wavelength section at each end, with an intervening quarter-wavelength phase reversal stub in between each new section, and the preceding section. Once you get longer than five half-wavelengths, which provides the 4.5-dB gain, the physical size becomes a bit of a bother for most folks.
From Book Practical Antenna Handbook - Joseph P. Carr
Double extended Zepp antenna
The double extended Zepp antenna (Fig. 6-19) provides a gain of about 2 dB over a dipole at right angles to the antenna wire plane. It consists of two sections of wire, each one of a length
Typical lengths are 20.7 ft on the 10-m band, 28 ft on the 15-m band, 42 ft on the 20-m band, and 84 ft on the 40-m band. The double extended Zepp antenna can be fed directly with 450-Ωtwin lead, especially if a balanced antenna tuner is available at the receiver. Alternatively, it can be fed from a quarter-wavelength matching section (made of 450-Ω twin lead, or equivalent open air parallel line), as shown, and a balun if coax is preferred. The length of the matching section should be
The double extended Zepp will work on several different bands. For example, a 20-m-band double extended Zepp will work as a Zepp on the design band, a dipole on frequencies below the design band, and as a four-lobed cloverleaf antenna on frequencies above the design band.
From Practical Antenna Handbook - Joseph P. Carr
Typical lengths are 20.7 ft on the 10-m band, 28 ft on the 15-m band, 42 ft on the 20-m band, and 84 ft on the 40-m band. The double extended Zepp antenna can be fed directly with 450-Ωtwin lead, especially if a balanced antenna tuner is available at the receiver. Alternatively, it can be fed from a quarter-wavelength matching section (made of 450-Ω twin lead, or equivalent open air parallel line), as shown, and a balun if coax is preferred. The length of the matching section should be
The double extended Zepp will work on several different bands. For example, a 20-m-band double extended Zepp will work as a Zepp on the design band, a dipole on frequencies below the design band, and as a four-lobed cloverleaf antenna on frequencies above the design band.
From Practical Antenna Handbook - Joseph P. Carr
Broadband Dipoles
One of the rarely discussed aspects of antenna construction is that the length/diameter ratio of the conductor used for the antenna element is a factor in determining the bandwidth of the antenna. In general, the rule of thumb states that large cross-sectional area makes the antenna more broadbanded. In some cases, this rule suggests the use of aluminum tubing instead of copper wire for the antenna radiator. On the higher-frequency bands that is a viable solution. Aluminum tubing can be purchased for relatively small amounts of money, and is both lightweight and easily worked with ordinary tools. But, as the frequency decreases, the weight becomes greater because the tubing is both longer and (for structural strength) must be of greater diameter. On 80 m, aluminum tubing is impractical, and at 40 m it is nearly so. Yet, 80 m is a significant problem, especially for older transmitters, because the band is 500 kHz wide, and the transmitters often lack the tuning range for the entire band. Some other solution is needed. Here are three basic solutions to the problem of wide-bandwidth dipole antennas: folded dipole, bowtie dipole, and cage dipole.
Figure 6-10A shows the folded dipole antenna. This antenna basically consists of two half-wavelength conductors shorted together at the ends and fed in the middle of one of them. The folded dipole is most often built from 300-Ω television antenna twin-lead transmission line. Because the feedpoint impedance is nearly 300 Ω, the same type of twin lead can also be used for the transmission line. The folded dipole will exhibit excellent wide-bandwidth properties, especially on the lower bands.
A disadvantage of this form of antenna is that the transmitter has to match the 300-Ω balanced transmission line. Unfortunately, most modern radio transmitters are designed to feed coaxial-cable transmission line. Although an antenna tuner can be placed at the transmitter end of the feedline, it is also possible to use a 4:1 balun transformer at the feedpoint (Fig. 6-10B). This arrangement makes the folded dipole a reasonable match to 52- or 75-Ω coaxial-cable transmission line.
Another method for broadbanding the dipole is to use two identical dipoles fed from the same transmission line, and arranged to form a “bowtie” as shown in Fig. 6-11. The use of two identical dipole elements on each side of the transmission line has the effect of increasing the conductor cross sectional area so that the antenna has a slightly improved length/diameter ratio.
The bowtie dipole was popular in the 1930s and 1940s, and became the basis for the earliest television receiver antennas (TV signals are 3 to 5 MHz wide, so they require a broadbanded antenna). It was also popular during the 1950s as the so-called Wonder Bar antenna for 10 m. It still finds use, but it has faded somewhat in popularity.
The cage dipole (Fig. 6-12) is similar in concept, if not construction, to the bowtie. Again, the idea is to connect several parallel dipoles together from the same transmission line in an effort to increase the apparent cross-sectional area. In the case of the cage dipole, however, spreader disk insulators are constructed to keep the wires separated. The insulators can be built from plexiglass, lucite, or ceramic.
They can also be constructed of materials such as wood, if the wood is properly treated with varnish, polyurethene, or some other material that prevents it from becoming waterlogged. The spreader disks are held in place with wire jumpers (see inset to Fig. 6-12) that are soldered to the main element wires.
A tactic used by some builders of both bowtie and cage dipoles is to make the elements slightly different lengths. This “stagger tuning” method forces one dipole to favor the upper end of the band, and the other to favor the lower end of the band. The overall result is a slightly flatter frequency response characteristic across the entire band. On the cage dipole, with four half-wavelength elements, it should be possible to overlap even narrower sections of the band in order to create an even flatter characteristic.
From Book : Practical Antenna Handbook - Joseph P. Carr
Figure 6-10A shows the folded dipole antenna. This antenna basically consists of two half-wavelength conductors shorted together at the ends and fed in the middle of one of them. The folded dipole is most often built from 300-Ω television antenna twin-lead transmission line. Because the feedpoint impedance is nearly 300 Ω, the same type of twin lead can also be used for the transmission line. The folded dipole will exhibit excellent wide-bandwidth properties, especially on the lower bands.
A disadvantage of this form of antenna is that the transmitter has to match the 300-Ω balanced transmission line. Unfortunately, most modern radio transmitters are designed to feed coaxial-cable transmission line. Although an antenna tuner can be placed at the transmitter end of the feedline, it is also possible to use a 4:1 balun transformer at the feedpoint (Fig. 6-10B). This arrangement makes the folded dipole a reasonable match to 52- or 75-Ω coaxial-cable transmission line.
Another method for broadbanding the dipole is to use two identical dipoles fed from the same transmission line, and arranged to form a “bowtie” as shown in Fig. 6-11. The use of two identical dipole elements on each side of the transmission line has the effect of increasing the conductor cross sectional area so that the antenna has a slightly improved length/diameter ratio.
The bowtie dipole was popular in the 1930s and 1940s, and became the basis for the earliest television receiver antennas (TV signals are 3 to 5 MHz wide, so they require a broadbanded antenna). It was also popular during the 1950s as the so-called Wonder Bar antenna for 10 m. It still finds use, but it has faded somewhat in popularity.
The cage dipole (Fig. 6-12) is similar in concept, if not construction, to the bowtie. Again, the idea is to connect several parallel dipoles together from the same transmission line in an effort to increase the apparent cross-sectional area. In the case of the cage dipole, however, spreader disk insulators are constructed to keep the wires separated. The insulators can be built from plexiglass, lucite, or ceramic.
They can also be constructed of materials such as wood, if the wood is properly treated with varnish, polyurethene, or some other material that prevents it from becoming waterlogged. The spreader disks are held in place with wire jumpers (see inset to Fig. 6-12) that are soldered to the main element wires.
A tactic used by some builders of both bowtie and cage dipoles is to make the elements slightly different lengths. This “stagger tuning” method forces one dipole to favor the upper end of the band, and the other to favor the lower end of the band. The overall result is a slightly flatter frequency response characteristic across the entire band. On the cage dipole, with four half-wavelength elements, it should be possible to overlap even narrower sections of the band in order to create an even flatter characteristic.
From Book : Practical Antenna Handbook - Joseph P. Carr
Sloping Dipole
The sloping dipole (Fig. 6-8) is popular with those operators who need a low angle of radiation, and are not overburdened with a large amount of land to install the antenna. This antenna is also called the sloper and the slipole in various texts. The author prefers the term “slipole,” in order to distinguish this antenna from a sloping vertical of the same name. Whatever it is called, however, it is a half-wavelength dipole that is built with one end at the top of a support, and the other end close to the
ground, and being fed in the center by coaxial cable. Some of the same comments as obtained for the inverted-vee antenna also apply to the sloping dipole, so please see that section also. Some operators like to arrange four sloping dipoles from the same mast such that they point in different directions around the compass (Fig. 6-9). A single fourposition coaxial cable switch will allow switching a directional beam around the compass to favor various places in the world.
From Practical Antenna Handbook - Joseph P Carr
ground, and being fed in the center by coaxial cable. Some of the same comments as obtained for the inverted-vee antenna also apply to the sloping dipole, so please see that section also. Some operators like to arrange four sloping dipoles from the same mast such that they point in different directions around the compass (Fig. 6-9). A single fourposition coaxial cable switch will allow switching a directional beam around the compass to favor various places in the world.
From Practical Antenna Handbook - Joseph P Carr
Inverted-Vee Dipole
The inverted-vee dipoleis a half-wavelength antenna fed in the center like a dipole. By the rigorous definition, the inverted-vee is merely a variation on the dipole theme. But in this form of antenna (Fig. 6-7), the center is elevated as high as possible from the earth’s surface, but the ends droop to very close to the surface. Angle a can be almost anything convenient, provided that a > 90 degrees; typically, most inverted-vee antennas use an angle of about 120 degrees. Although essentially a compensation antenna for use when the dipole is not practical, many operators believe that it is essentially a better performer on 40 and 80 m in cases where the dipole cannot be mounted at a half-wavelength (64 ft or so). By sloping the antenna elements down from the horizontal to an angle (as shown in Fig. 6-7), the resonant frequency is effectively lowered. Thus, the antenna will
By sloping the antenna elements down from the horizontal to an angle (as shown in Fig. 6-7), the resonant frequency is effectively lowered. Thus, the antenna will
need to be shorter for any given frequency than a dipole. There is no absolutely rigorous equation for calculation of the overall length of the antenna elements. Although the concept of “absolute” length does not hold for regular dipoles, it is even less viable for the inverted-vee. There is, however, a rule of thumb that can be followed for a starting point: Make the antenna about 6 percent shorter than a dipole for the same frequency. The initial cut of the antenna element lengths (each quarter wavelength) is L = ft [6.16]
After this length is determined, the actual length is found from the same cutand-try method used to tune the dipole in the previous section. Bending the elements downward also changes the feedpoint impedance of the antenna and narrows its bandwidth. Thus, some adjustment in these departments is in order. You might want to use an impedance matching scheme at the feedpoint, or an antenna tuner at the transmitter.
By sloping the antenna elements down from the horizontal to an angle (as shown in Fig. 6-7), the resonant frequency is effectively lowered. Thus, the antenna will
need to be shorter for any given frequency than a dipole. There is no absolutely rigorous equation for calculation of the overall length of the antenna elements. Although the concept of “absolute” length does not hold for regular dipoles, it is even less viable for the inverted-vee. There is, however, a rule of thumb that can be followed for a starting point: Make the antenna about 6 percent shorter than a dipole for the same frequency. The initial cut of the antenna element lengths (each quarter wavelength) is L = ft [6.16]
After this length is determined, the actual length is found from the same cutand-try method used to tune the dipole in the previous section. Bending the elements downward also changes the feedpoint impedance of the antenna and narrows its bandwidth. Thus, some adjustment in these departments is in order. You might want to use an impedance matching scheme at the feedpoint, or an antenna tuner at the transmitter.
The dipole feedpoint
The dipole is a half-wavelength antenna fed in the center. Figure 6-2 shows the voltage (V) and current (I) distributions along the length of the half-wavelength radiator element. The feedpoint is at a voltage minimum and a current maximum, so you can assume that the feedpoint is a current antinode.
At resonance, the impedance of the feedpoint is Ro = V/I.
There are two resistances that make up Ro. The first is the ohmic losses that generate nothing but heat when the transmitter is turned on. These ohmic losses come from the fact that conductors have electrical resistance and electrical connections are not perfect (even when properly soldered). Fortunately, in a well-made dipole these losses are almost negligible.
The second contributor is the radiation resistance Rr of the antenna. This resistance is a hypothetical concept that accounts for the fact that RF power is radiated by the antenna. The radiation resistance is the fictional resistance that would dissipate the amount of power that is radiated away from the antenna.
For example, suppose we have a large-diameter conductor used as an antenna, and it has negligible ohmic losses. If 1000 W of RF power is applied to the feedpoint, and a current of 3.7 A is measured, what is the radiation resistance?

It is always important to match the feedpoint impedance of an antenna to the transmission-line impedance. Maximum power transfer always occurs (in any system) when the source and load impedances are matched. In addition, if some applied power is not absorbed by the antenna (as happens in a mismatched system), then the unabsorbed portion is reflected back down the transmission line toward the transmitter. This fact gives rise to standing waves, and the so-called standing wave ratio (SWR or VSWR) discussed in Chap. 3. This is a problem to overcome. Matching antenna feedpoint impedance seems to be simplicity itself because the free-space feedpoint impedance of a simple dipole is about 73 Ω, seemingly a good match to 75-Ω coaxial cable. Unfortunately, the 73-Ω feedpoint impedance is almost a myth. Figure 6-3 shows a plot of approximate radiation resistance (Rr) versus height above ground (as measured in wavelengths). As before, we deal in approximations in Fig. 6-3; in this case, the ambiguity is introduced by ground losses. Despite the fact that Fig. 6-3 is based on approximations, you can see that radiation resistance varies from less than 10 Ω, to around 100 Ω, as a function of height. At heights of many wavelengths, this oscillation of the curve settles down to the freespace impedance (72 Ω). At the higher frequencies, it might be possible to install a dipole at a height of many wavelengths. In the 2-m amateur radio band (144 to 148 MHz), one wavelength is around 6.5 ft (i.e., 2 m ×3.28 ft/m), so “many wavelengths” is relatively easy to achieve at reasonably attainable heights. In the 80-m band (3.5 to 4.0 MHz), however, one wavelength is on the order of 262 ft, so “many wavelengths” is a practical impossibility. There are three tactics that can be followed. First, ignore the problem altogether. In many installations, the height above ground will be such that the radiation resistance will be close enough to present only a slight impedance mismatch to a standard coaxial cable. The VSWR is calculated (among other ways) as the ratio:
good engineering practice (there are sometimes practical reasons) it is nonetheless necessary to install a dipole at less than optimum height. So, if that becomes necessary, what are the implications of feeding a 60-Ω antenna with either 52- or 75-Ω standard coaxial cable? Some calculations are revealing: For 75-Ω coaxial cable:
In neither case is the VSWR created by the mismatch too terribly upsetting. The second approach is to mount the antenna at a convenient height, and use an impedance matching scheme to reduce the VSWR. In Chap. 23, you will find information on various suitable (relatively) broadbanded impedance matching methods including Q-sections, coaxial impedance transformers, and broadband RF transformers.“Homebrew” and commercially available transformers are available to cover most impedance transformation tasks. The third approach is to mount the antenna at a height (Fig. 6-3) at which the expected radiation resistance crosses a standard coaxial cable characteristic impedance. The best candidate seems to be a height of a half-wavelength because the radiation resistance is close to the free-space value of 72 Ω, and is thus a good match for 75-Ω coaxial cable (such as RG-11/U or RG-59/U).
From Practical Antenna Handbook : Joseph J. Carr
At resonance, the impedance of the feedpoint is Ro = V/I.
There are two resistances that make up Ro. The first is the ohmic losses that generate nothing but heat when the transmitter is turned on. These ohmic losses come from the fact that conductors have electrical resistance and electrical connections are not perfect (even when properly soldered). Fortunately, in a well-made dipole these losses are almost negligible.
The second contributor is the radiation resistance Rr of the antenna. This resistance is a hypothetical concept that accounts for the fact that RF power is radiated by the antenna. The radiation resistance is the fictional resistance that would dissipate the amount of power that is radiated away from the antenna.
For example, suppose we have a large-diameter conductor used as an antenna, and it has negligible ohmic losses. If 1000 W of RF power is applied to the feedpoint, and a current of 3.7 A is measured, what is the radiation resistance?

It is always important to match the feedpoint impedance of an antenna to the transmission-line impedance. Maximum power transfer always occurs (in any system) when the source and load impedances are matched. In addition, if some applied power is not absorbed by the antenna (as happens in a mismatched system), then the unabsorbed portion is reflected back down the transmission line toward the transmitter. This fact gives rise to standing waves, and the so-called standing wave ratio (SWR or VSWR) discussed in Chap. 3. This is a problem to overcome. Matching antenna feedpoint impedance seems to be simplicity itself because the free-space feedpoint impedance of a simple dipole is about 73 Ω, seemingly a good match to 75-Ω coaxial cable. Unfortunately, the 73-Ω feedpoint impedance is almost a myth. Figure 6-3 shows a plot of approximate radiation resistance (Rr) versus height above ground (as measured in wavelengths). As before, we deal in approximations in Fig. 6-3; in this case, the ambiguity is introduced by ground losses. Despite the fact that Fig. 6-3 is based on approximations, you can see that radiation resistance varies from less than 10 Ω, to around 100 Ω, as a function of height. At heights of many wavelengths, this oscillation of the curve settles down to the freespace impedance (72 Ω). At the higher frequencies, it might be possible to install a dipole at a height of many wavelengths. In the 2-m amateur radio band (144 to 148 MHz), one wavelength is around 6.5 ft (i.e., 2 m ×3.28 ft/m), so “many wavelengths” is relatively easy to achieve at reasonably attainable heights. In the 80-m band (3.5 to 4.0 MHz), however, one wavelength is on the order of 262 ft, so “many wavelengths” is a practical impossibility. There are three tactics that can be followed. First, ignore the problem altogether. In many installations, the height above ground will be such that the radiation resistance will be close enough to present only a slight impedance mismatch to a standard coaxial cable. The VSWR is calculated (among other ways) as the ratio:
good engineering practice (there are sometimes practical reasons) it is nonetheless necessary to install a dipole at less than optimum height. So, if that becomes necessary, what are the implications of feeding a 60-Ω antenna with either 52- or 75-Ω standard coaxial cable? Some calculations are revealing: For 75-Ω coaxial cable:
In neither case is the VSWR created by the mismatch too terribly upsetting. The second approach is to mount the antenna at a convenient height, and use an impedance matching scheme to reduce the VSWR. In Chap. 23, you will find information on various suitable (relatively) broadbanded impedance matching methods including Q-sections, coaxial impedance transformers, and broadband RF transformers.“Homebrew” and commercially available transformers are available to cover most impedance transformation tasks. The third approach is to mount the antenna at a height (Fig. 6-3) at which the expected radiation resistance crosses a standard coaxial cable characteristic impedance. The best candidate seems to be a height of a half-wavelength because the radiation resistance is close to the free-space value of 72 Ω, and is thus a good match for 75-Ω coaxial cable (such as RG-11/U or RG-59/U).
From Practical Antenna Handbook : Joseph J. Carr
Simple Halfwave Dipole Antennas
The simple dipole, or doublet, is a case in point. This antenna is also sometimes called the Hertz, or hertzian, antenna because radio pioneer Heinrich Hertz reportedly used this form in his experiments. The half-wavelength dipole is a balanced antenna consisting of two radiators (Fig. 6-1) that are each a quarter-wavelength, making a total of a half-wavelength. The antenna is usually installed horizontally with respect to the earth’s surface, so it produces a horizontally polarized signal.
Let say you have L long dipole antenna .
for halfwave dipole antenna L = 1/2L = 1/4 L + 1/4L
In its most common configuration (Fig. 6-1), the dipole is supported at each end by rope and end insulators. The rope supports are tied to trees, buildings, masts, or some combination of such structures. The length of the antenna is a half-wavelength. Keep in mind that the physical length of the antenna, and the theoretical electrical length, are often different by about 5 percent. A free-space half-wavelength is found from
L = 492/Fmhz feet [6.1]

In a perfect antenna, that is self-supported many wavelengths away from any object, Eq. 6.1 will yield the physical length. But in real antennas, the length calculated above is too long. The average physical length is shortened by up to about 5 percent because of the velocity factor of the wire and capacitive effects of the end insulators. A more nearly correct approximation (remember that word, it's important) of a half-wavelength antenna is
L = 468/Fmhz ft [6.2]
where L is the length of a half-wavelength radiator, in feet F MHz is the operating frequency, in megahertz
Example Calculate the approximate physical length for a half-wavelength dipole operating on a frequency of 7.25 MHz. Solution:
L = 468/Fmhz ft
= 468/7.25 ft
= 64.55 ft
or, restated another way:
L = 64 ft 6.6 in
It is unfortunate that a lot of people accept Eq. 6.2 as a universal truth, a kind of immutable law of The Universe. Perhaps abetted by books and articles on antennas that fail to reveal the full story, too many people install dipoles without regard for reality. The issue is resonance. An antenna is a complex RLC network. At some frequency, it will appear like an inductive reactance (X = +jXL), and at others it will appear like a capacitive reactance (X =–jXC). At a specific frequency, the reactances are equal in magnitude, but opposite in sense, so they cancel each other out: XL – XC = 0. At this frequency, the impedance is purely resistive, and the antenna is said to be resonant. The goal in erecting a dipole is to make the antenna resonant at a frequency that is inside the band of interest, and preferably in the portion of the band most often used by the particular station. Some of the implications of this goal are covered later on, but for the present, assume that the builder will have to custom-tailor the length of the antenna. Depending on several local factors (among them, nearby objects, the shape of the antenna conductor, and the length/diameter ratio of the conductor) it might prove necessary to add, or trim, the length a small amount to reach resonance.

Let say you have L long dipole antenna .
for halfwave dipole antenna L = 1/2L = 1/4 L + 1/4L
In its most common configuration (Fig. 6-1), the dipole is supported at each end by rope and end insulators. The rope supports are tied to trees, buildings, masts, or some combination of such structures. The length of the antenna is a half-wavelength. Keep in mind that the physical length of the antenna, and the theoretical electrical length, are often different by about 5 percent. A free-space half-wavelength is found from
L = 492/Fmhz feet [6.1]
In a perfect antenna, that is self-supported many wavelengths away from any object, Eq. 6.1 will yield the physical length. But in real antennas, the length calculated above is too long. The average physical length is shortened by up to about 5 percent because of the velocity factor of the wire and capacitive effects of the end insulators. A more nearly correct approximation (remember that word, it's important) of a half-wavelength antenna is
L = 468/Fmhz ft [6.2]
where L is the length of a half-wavelength radiator, in feet F MHz is the operating frequency, in megahertz
Example Calculate the approximate physical length for a half-wavelength dipole operating on a frequency of 7.25 MHz. Solution:
L = 468/Fmhz ft
= 468/7.25 ft
= 64.55 ft
or, restated another way:
L = 64 ft 6.6 in
It is unfortunate that a lot of people accept Eq. 6.2 as a universal truth, a kind of immutable law of The Universe. Perhaps abetted by books and articles on antennas that fail to reveal the full story, too many people install dipoles without regard for reality. The issue is resonance. An antenna is a complex RLC network. At some frequency, it will appear like an inductive reactance (X = +jXL), and at others it will appear like a capacitive reactance (X =–jXC). At a specific frequency, the reactances are equal in magnitude, but opposite in sense, so they cancel each other out: XL – XC = 0. At this frequency, the impedance is purely resistive, and the antenna is said to be resonant. The goal in erecting a dipole is to make the antenna resonant at a frequency that is inside the band of interest, and preferably in the portion of the band most often used by the particular station. Some of the implications of this goal are covered later on, but for the present, assume that the builder will have to custom-tailor the length of the antenna. Depending on several local factors (among them, nearby objects, the shape of the antenna conductor, and the length/diameter ratio of the conductor) it might prove necessary to add, or trim, the length a small amount to reach resonance.
Subscribe to:
Comments (Atom)